Numerical stabilization techniques are often employed in under-resolved simulations of convection-dominated flows to improve accuracy and mitigate spurious oscillations. Specifically, the evolve--filter--relax (EFR) algorithm is a framework which consists in evolving the solution, applying a filtering step to remove high-frequency noise, and relaxing through a convex combination of filtered and original solutions. The stability and accuracy of the EFR solution strongly depend on two parameters, the filter radius 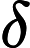  and the relaxation parameter  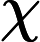. Standard choices for these parameters are usually fixed in time, and related to the full order model setting, i.e., the grid size for  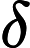 and the time step for  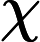. 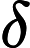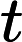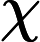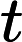The key novelties with respect to the standard EFR approach are: (i) time-dependent parameters   and  , and (ii) data-driven adaptive optimization of the parameters in time, considering a fully-resolved simulation as reference. In particular, we propose three different classes of optimized-EFR (Opt-EFR) strategies, aiming to optimize one or both parameters. The new Opt-EFR strategies are tested in the under-resolved simulation of a turbulent flow past a cylinder at  . 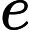The Opt-EFR proved to be more accurate than standard approaches by up to 99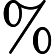 , while maintaining a similar computational time. In particular, the key new finding of our analysis is that such accuracy can be obtained only if the optimized objective function includes: (i) a global metric (as the kinetic energy), and (ii) spatial gradients' information.